φ (phi), also known as the Golden Ratio, was thought by the ancient Pythagoreans to have mystical properties. Even the more level-headed Greeks ascribed it artistic ones, for instance considering the most eye-pleasing rectangle to be one where the ratio of the long side to the short side is φ. As shown above, The Last Supper the Mona Lisa contains many golden rectangles.
They also have the nice property that if you divide one into a square and another, smaller rectangle, the new rectangle is also golden.
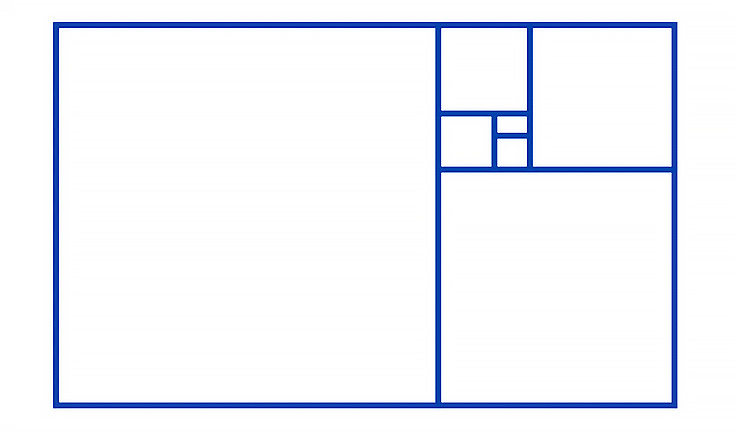
This gives us a clue for how to find φ: call the larger side of a golden rectangle a and the smaller side b. Once we carve out a square of size b, what’s left is a rectangle with large side b and small side a-b. Since that’s also golden, we know that:
(1) a/b = b/(a-b)
or, cross-multiplying
(2) b^2 = a^2 – ab
(3) 1 = (a/b)^2 – (a/b)
recognizing that a/b is φ and putting everything on one side,
(4) φ^2 – φ – 1 = 0
Applying the quadratic formula gives us
(5) φ = (1 +- √5)/2
At the moment we’re only interested in the positive solution, so
(6) φ = (1 + √5) / 2 ≈ 1.618
φ is interesting arithmetically too. Consider the Fibonacci sequence, which begins with two 1s, and thereafter makes new members by adding the previous two members:
1, 1, 2, 3, 5, 8, 13, 21, 34, …
The sequence of ratios of two adjacent Fibonacci numbers begins:
1, 2, 1.5, 1.666, 1.6, 1.625, 1.615, 1.619, …
It’s not hard to prove that this ratio converges to φ. It (almost) doesn’t matter what the first two numbers are: the ratios still converge to φ. Let’s do something outlandish like -17 and 12:
-17, 12, -5, 7, 2, 9, 11, 20, 31, 51, 82, 133…
The ratios are:
-.706, -.417, -1.4, .286, 4.5, 1.222, 1.55, 1.645, 1.608, 1.622
The ratios start out all over the place, but converge towards φ soon.
Since from (4), above, φ^2 = φ + 1, we could also start with the numbers 1 and φ to build an additive sequence whose ratios are all φ:
(A) 1, φ, φ + 1, 2φ + 1, 3φ + 2, 4φ + 3, …
which is identical to
1, φ, φ^2, φ^3, φ^4, φ^5, …
So, do the ratios of all additive sequences converge to φ? As I said above, almost. There’s one exception, based on the other solution to the quadratic (5): (1 – √5) / 2 ≈ -0.618 . For now, let’s call this ψ. It’s easy to verify a few things about ψ:
(7) ψ = -1/φ
(8) ψ = -(φ-1)
(9) ψ^2 = ψ + 1
The last of these means we’ve found an additive sequence whose ratio isn’t φ:
(B) 1, -1/φ, 1/φ^2, -1/φ^3, 1/φ^4, …
The ratio is always exactly -1/φ. In fact, that’s the only such sequence, and the numbers have to be exact. If we start even a little bit off, say with 1 and -.6, we get:
1, -.6, .4, -.2, .2, 0, .2, .2, .4, .6, 1.0, 1.6, …
At this point we have the regular Fibonacci sequence with each term multiplied by .2, so we know the ratios will go towards φ. In fact, if you calculate (B) on a computer and print out the ratios, you’ll find them going towards φ, because a computer doesn’t do exact arithmetic, and the little bits of roundoff error are sufficient to push it over the edge.
So we’ve found an important difference between φ and -1/φ:
- An additive sequence whose initial ratio is φ will keep the ratio φ
- An additive sequence whose initial ratio is -1/φ will keep the ratio -1/φ
- An additive sequence whose initial ratio is anything else will converge towards the ratio φ
That is, the sequence with ratio φ is stable (also called an attractor), while the sequence with ratio -1/φ is unstable. Another way to look at this is that any additive sequence is a linear combination of (A) and (B). Since the terms in A tend towards infinity while the terms in B tend towards 0, the only way for A not to dominate B is for the sequence to be all B with no A.
This doesn’t even scratch the surface of the things to be said about φ, but it’ll do for now.
I’ve read that a lot of so called examples of golden ratios are not, in fact, golden ratios, but are either things that are close to or approximate the golden ratio or outright lies.
For instance, notice the 7 green rectangles above Jesus’ head. They can’t possibly be all golden rectangles: they’re all of the same height but have varying widths, meaning the ratio between their long sides and short sides are unequal.
So, unless I’m misunderstanding something about either the golden ratio or what that picture purports to represent, it seems like another example of exaggerating the importance of the former.
You know, you’re right. Very few of those rectangles look golden to me. That picture is trying to show different sorts of mathematical relationships, but it got mislabeled in the web site I took it from, and I propagated the error. I’m going to replace it with a picture of the Mona Lisa where the rectangles are golden.
Cool.
But see… even there… it just looks like they’ve overlaid some golden rectangles that don’t actually correspond to anything. For instance, take that upper left rectangle, itself comprised of 5 smaller ones. The height corresponds almost perfectly to her head -COOL!- but the width doesn’t really line up.
A bit of Google-sleuthing indicates that the ML might contain golden proportions, but not necessarily golden rectangles. And maybe that image does indicate that and I’m just reading it wrong. I was once a math person, way back in high school, and remembered studying all this stuff, but lost most of my working knowledge of it once I hit college and started studying the inner workings of elementary school math (equally fascinating in their own right, but a different ball of wax altogether).
And I hate to be such a nitpicker… but this is how I learn math. If my teacher told us something and it didn’t make sense… not just from a confusion standpoint but from a “I think I do understand this and it’s telling me something different” standpoint, I had to pester until they either made it made sense or until I proved thousands of years of math theorems wrong.
It was usually the former.
Yeah, the Mona Lisa’s more about golden ratios and golden spirals. Imagine a spiral starting in the smallest square and arcing out through all the squares. It starts on her nose, touches the edge of her smile, cups her chin, the top of her head, and then comes to rest in the sleeve of her right hand.
This is awesome. I demand more math posts!
I really hate that I lost most of the math knowledge that I learned in school. Its not something that I need to do everyday but I wish I could still do and understand algebra, trigonometry, geometry, and pre-calculus. I could read a bit of this post but not enough.
Oh, and now I’ll share a funny math anecdote my high school math teacher shared every other day.
She wrote “5!” on the board and asked her students what it said.
One confident young man rose his hand and said, “FIVE!!!”
She could barely get through the story without falling down laughing. Math humor…
I can’t believe I didn’t write this post about my favorite number! Oh yeah! I never write posts that I intend to write!
Anyway, if you liked this post, I highly recommend The Divine Proportion. There are other books on the topic that I haven’t read that may be as good or better, but this one definitely has the flavor of Mike’s post here.